The Monochord.

Until recently, I had some difficulty explaining the origin of the link between music and science. Of course, I understood this deep connection, that frequencies are ultimately numbers, and they relate to each other in rational intervals. This understanding is due to the fascinating fact that the ear has both qualitative and quantitative abilities: it has the ability to understand the moods/colors and the ratios of sounds. This ability makes it a pretty unique sense; in fact, it is the only sense that can accurately measure and “feel” at the same time.

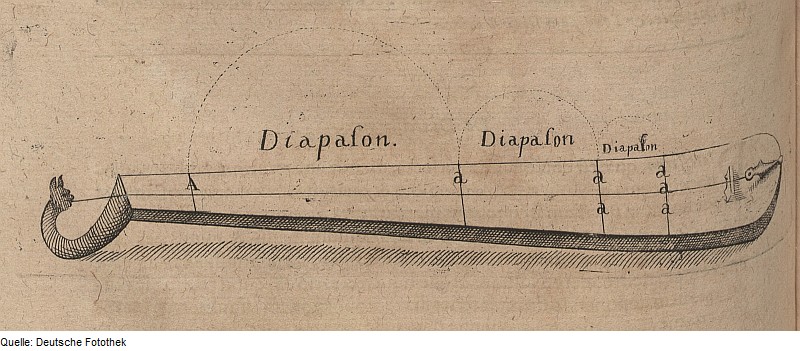
But this did not explain that since antiquity, music was made an equal to geometry, mathematics and astronomy (The Quadrivium); it is only recently in the modern era that we are able to understand frequencies and compute them, and this is only made possible by the use of scientific instruments. Although ratios between the partials were understood to be rational in their fundamental nature: 1:2, 2:3 and 3:4 for the octave, 5th, 4th, and so on, that knowledge dates from antiquity. But how did this realization come about? I was aware of the monochord but I took it as a demonstration tool, illustrating the phenomena of musical ratios. I had it wrong: the monochord is not the message, it is the medium. It is the “instrument” that led to this discovery, and in fact, the monochord is the first scientific instrument which allowed accurate measuring of a physical phenomena, to display geometrically these acoustic relationships and to translate them mathematically. The origin of the monochord is unknown: “the Greeks attributed its invention to Pythagorus; however, like most musical technologies it was probably imported from Babylonia or Egypt…No more accurate tool for investigating musical tuning was invented after the research of Helmholtz in the later half of the nineteenth century.” [An Introduction to the Monochord, Seimen Terpstra]

Modern monochord with four strings

Initially what the monochord was able to investigate is the rational division of the whole. This term is taken as “wholly” a quasi-“god”- like concept, in a cosmological sense. In other words, the rational division visually demonstrated by the placement of the “bridges” dividing the strings at various divisions of the “whole”, illustrated the inner working of the cosmos, revealing the inner harmonies of the world that were at the core of philosophical inquiry up to the nineteenth century.

Back in antiquity, truth for the Pythagoreans manifests itself through the world of physical phenomena. (Fideler in Guthrie, 1987) “The Number was the essence of a sacred order, and nowhere was this better expressed for the Pythagoreans than in cosmic music, paradoxically unperceivable because [it was] permanent.” (“Star Music”, Eduard C. Heyning, 2017)

“As the eyes are designed to look up at the stars, so are the ears to hear harmonious motions; and these are sister sciences – as the Pythagoreans say.” (Plato Republic VII 530d; 1937, I. 790)

Boethius

“The ears of mortals are filled with this sound, but they are unable to hear it….The sound coming from the heavenly spheres revolving at very swift speeds is of course so great that human ears cannot catch it; you might as well try to stare directly at the sun, whose rays are much too strong for your eyes.” (Cicero, The Dream of Scipio),

So this music of the spheres is music that we cannot hear because we’ve been hearing it since birth. Only the semi-divine Pythagorus could, and he was able to make us hear and see on a string, this music to which the planets of the solar system who can be made to intone a dominant chord, (see “Waves Passing in the Night”, Walter Murch). What can it reveal to us?

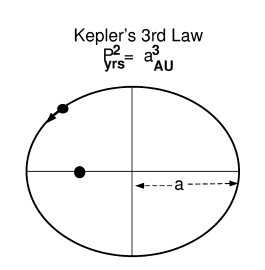
Kepler 3rd (Harmonic) law

Closer to us in history, Johannes Kepler is the one who began to bridge the two world views of wholistic antiquity and the birth of modern science. Kepler is a “rational mystic”: in one way looking back over the centuries to the platonic theories, and in the other, laying down the laws of planetary motion which generated the foundation for the future work of Newton on the laws of gravity. This is culminated in Kepler’s third law, which rules that the ratios between the semi-axis (half the diameter) of the orbit of a planet and the period (a planet’s path around the Sun in a year) is harmonically related (r³= P²). This third law of Kepler’s is called “the harmonic law”, which has one foot in antiquity and the other in the modern world. 

As it turns out, many examples of harmonic relationships exist in astronomy. The most evident example that illustrates this relation and that we can all witness in the sky, is the 1:1 relationship locking the Moon to the Earth (one revolution = one rotation) so that we can only see one face of our satellite (incidentally, many exoplanets are gravitationally locked to their stars); another more distant example are the three inner moons of Jupiter which are in a 1:1, 2:1 and 4:1 harmonic lock, with their rotation also, like our Moon, on a 1:1 relationship with their revolution around Jupiter.“Jupiterians” would see only one side of each of these moons.

These relationships arise from the reciprocal gravitational influences of these celestial bodies; although they are harmonic in essence, they arise from different processes than musical harmonics. On the other hand, both share a surprising consistency with whole numbers.

Pythagorus

Further numerical musings about whole numbers and speculations have been made, and are probably the root of numerology. Pythagorus was obsessed with whole numbers; he realized that the sum of 1, 2, 3 and 4 make 10 and went on from there to many speculations about the number ten. Of course there is the theorem that bears his name: 3² + 4² = 5² which probably set the standard for “beauty” in mathematical formulas. Going back to the monochord, my point is that simple rational relationships of integers are at the base of both music and science – astronomy in this case, and that, interestingly enough, in the process of codification of these disciplines, music did precede or at least showed the way.

These whole numbers are in use in the ratios visually displayed on the monochord from the root, fifth, fourth, third and so on to build scales…as 1, 2, 3, 4… although to say the astronomical and musical harmonics are one and the same seems enticing, until we understand more about both phenomenas, the jury is still out. Also, it is important to note that there are many incommensurablities. The “pythagorus comma” is a good example (the sum of twelve fifths = B#; this does not add up to the sum of 7 octaves = C8).

To summarize, these “explorations” were initiated with this perfect hybrid: the monochord, which is an “instrument,” a word used both to describe the tools to conduct science and music, and are etymologically linked for a good reason.