Category Archives: Science & Music

The links between science and music (and art to a wider extent) is by far not a new concept, you can actually hold an argument that they were united in most of their history, as science and art were both considered as philosophy.

Painted Rock: a natural alignment with Chumash cosmology

Featured

Posted on by
Reply

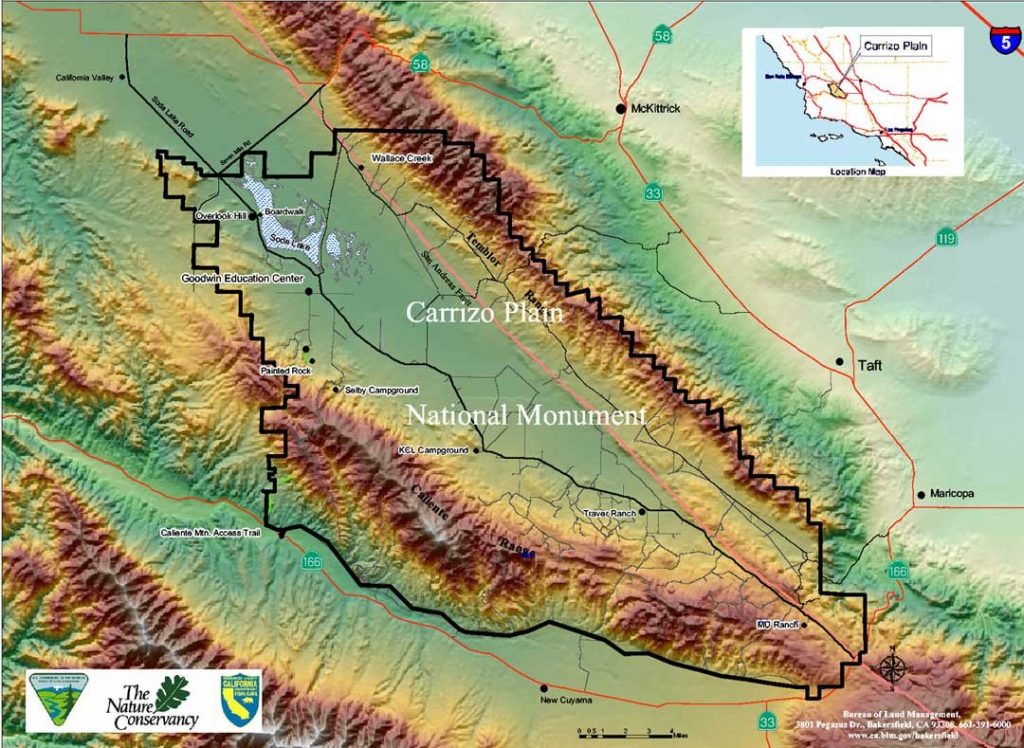
In the heart of California’s Carrizo Plain National Monument, an ancient natural formation known as Painted Rock stands as a testament to the region’s rich cultural and ecological history. For centuries, the Chumash people painted many petroglyphs on it inside walls and regarded this site as a sacred place, using it for ceremonies, initiations, and astronomical observations. Recent observations reveal an extraordinary feature of Painted Rock: its alignment with key celestial events, echoing the cosmology of the Chumash in remarkable ways.

The Chumash were a highly advanced and vibrant society whose territory stretched from Malibu Beach in the south to the central regions of San Luis Obispo County in the north, bordered by the Carrizo Plain and Mount Piños to the east (the highest peak in the region at 8,831 feet), and the Channel Islands to the west. Archaeological evidence shows that the Chumash settled in the Carrizo Plain as early as 2000 BCE, with their population peaking around 1000 CE. However, the population diminished steeply after that, likely due to significant climate changes that affected the region’s resources, Some Peoples from the Yokuts settled and shared the area until the 19th century.

The Carrizo Plain is bordered on the east by the San Andreas Fault, a geographical feature that not only shaped the landscape but also influenced the water sources and ecosystems the Chumash depended upon. Painted Rock, located near the heart of the plain, became a spiritual and cultural focal point for the Chumash people.

Chumash cosmology divided the universe into three interconnected realms: the underworld, the middle world, and the sky world. Humans inhabited the middle world and were tasked with maintaining balance between the realms, which were permeated by a neutral energy. Unlike many cultures that revered the Sun, the Chumash held the North Star (Polaris) as the most significant celestial object, symbolizing stability and balance in the universe.

A map of the Carrizo Plain National Monument. You can see the location of Painted Rock on the center right.

“California’s Chumash Indians thought of the sky gods this way. They saw a balance of nature and the world order in terms of a nightly gambling game played between two teams. Sun was the captain of one team, while the pole star, Polaris, led the other. Polaris was known as Sky Coyote, and its pivotal position among the stars made it a symbol of the night.

For a full year they played, and at the winter solstice the score was tallied. Moon, that expert at counting out the days, kept score. If, at the winter solstice, Sun was the winner, it would go bad for people on earth: rather than return upon his yearly journey back to the north, he might just continue on south and leave the earth in the dead of winter, with the cosmos out of balance. Sky Coyote was a benefactor, a benevolent influence. If his team won, the order of things would be restored.” E.C. Krupp Echoes of the Ancient Skies

A Petroglyph of the Sky Coyote on the inside of Painted Rock (unfortunately damaged like many of the other painting on the rock ) photo by Dan McCaslin / Noozhawk

My wife, Sarah Pillow, and I have been visiting the Carrizo Plain for many years, drawn by its unspoiled landscapes, pristine night skies, and rich history. Our connection to the area deepened through stargazing and learning about the indigenous Chumash culture, so vividly demonstrated at the Painted Rock monument. As an amateur astronomer with a passion for sky lore and archeo-astronomy, I was particularly intrigued by how the Chumash integrated celestial events into their cultural practices.

In August 2023, I conducted a detailed scan of the interior of Painted Rock using an iPhone and the Scaniverse app. The scan data was assembled in Blender, and I also created a 360˚ panoramic photo of the site, which I inserted into the Stellarium app for astronomical analysis. The results were striking: the rock formation, shaped like a large horseshoe, has its opening perfectly oriented towards Polaris, a celestial body of profound significance in Chumash cosmology. (see below a short video that show the North view of a whole year motion of the constelation around Polaris)

whole year motion of the constelation around Polaris

Another remarkable discovery emerged during my analysis: on the south side of Painted Rock, the Sun at noon during the winter solstice aligns precisely with the top of the formation. This natural alignment mirrors the Chumash’s understanding of celestial cycles, which informed their rituals and worldview. (see below a short video of the Sun, during a whole year at noon, looking south from inside the rock)

video of the Sun, during a whole year at noon, looking south from inside the rock

What makes this discovery particularly fascinating is that Painted Rock is a natural formation, not a human-made structure. Its alignment with these celestial events appears to be a fortuitous occurrence, yet it seamlessly supports the Chumash belief system. It highlights the deep connection the Chumash people saw between their sacred geography and the cosmos.

An aerial of Painted Rock

Tragically, the Chumash population was devastated during colonization. The establishment of Spanish missions introduced disease, forced labor, and cultural disruption, and westward expansion by settlers led to further extermination of their population and heritage. Yet, the Chumash legacy endures through their artifacts, traditions, and the profound cosmological insights that continue to inspire and amaze.

Part of a large painting on the inner wall of Painted Rock, unfortunately vandalized modern inhabitant of the area (the location is now fenced in and you need to register to visit it)

The Carrizo Plain is more than just the home of Painted Rock. It is a vital ecological and cultural preserve, with vibrant wildflower blooms, rare wildlife, and one of California’s last native grasslands. Its dark, unpolluted skies make it an ideal destination for stargazers and those seeking to connect with the celestial traditions of the past.

I hope this discovery inspires further exploration of Painted Rock and its connections to the Chumash worldview. By uncovering and honoring the interplay between culture, nature, and astronomy, we can better appreciate the profound legacy of the Chumash and their relationship with the universe. If you are fortunate enough to visit the Carrizo Plain, approach Painted Rock with reverence, keeping in mind its cultural and spiritual significance. Together, we can ensure this sacred site remains a source of wonder and learning for generations to come.

MUSIC COMMUNALITIES AND DIFFERENCES: SOCIOLOGY THROUGH SOUND

Featured

Posted on by
Reply

How do different cultures hear consonances; what are the facts that affect our perceptions and how might a word we use change if it is spoken or sung?


Is the way we hear and sing music unique to all ethnicities? And why, as we become aware by listening to music from around the world, do these differences and similarities arise? What follows is a summarization of two studies on this topic.

1. Communalities (consonances)

In the first study, the art of music is universal: comparative studies made on the subject show that there are underlining patterns that exist across cultures. In almost all of them, we find that the pitch of spoken and sung words have several different behaviors. For example, sung words are produced at a higher pitch; the pace of the word is slower; and the pitch is more stable than when the words are spoken.


In a paper on anthropology in Science Advances, the author put these facts to the test:
https://www.science.org/doi/10.1126/sciadv.adm9797


Concerning the pitch of a word, the article states: “we realized that in speech we recognize phonemes by the shape of formants (formants are an analysis of the component frequencies that make up human speech). These formants characterize how upper harmonics’ content is emphasized or attenuated. In speech, the frequency content that is conveying information is not fundamental frequency but harmonics; whereas in music, it is the lower fundamental frequencies that contain the crucial melodic content. We speculate that the difference in emphasis on formants versus fundamental frequency may underlie the difference in pitch height between speech and music we have identified.”


The “use of longer acoustic phrases, greater sound pressure, and less noisy sounds may ease the intelligibility of pitch information. This increased loudness and salience might also support evolutionary propositions that music evolved as a mnemonic device or as a night-time, long-distance communication device. The lyrics of the chosen songs [of the study] frequently mention “night,” “moon,” “sleep,” and “love,” which may further support the nocturnal hypothesis.”

Here’s a word cloud that illustrates this point:


To recapitulate features that the study identified as differentiating music and speech along a musi-linguistic continuum are pitch height, temporal rate, and pitch stability.
Since utilization of pitch can also be found in language (e.g., tonal languages: increasing the pitch of the final word in an interrogative sentence in today’s English and Japanese), inclusively probing what we can communicate with pitch in human acoustic communication may give insights into the fundamental nature of songs.


Meanwhile, the features identified as shared between speech and song—particularly timbral brightness and pitch interval size— represent promising candidates for understanding the role of vocalization that may shape the cultural evolution of music and language. Together, these cross-cultural similarities and differences may help shed light on the cultural and biological evolution of two systems that make us human: music and language.

2. Differences (dissonances)

The debate about following perfect mathematical rules, which was supported by all the followers of the strict tuning rules established by Pythagoras and based on the natural harmonic series, started to be questioned by the end of the Renaissance. The musicians of the time became more inclined to follow their ears and bend the strict rules to attain smoother relationships between the notes of the scale. In any case, these strict rules were never completely followed, as is clear when listening and comparing Western to Chinese and South Asian music. This study is addressing how these different tunings came to be used around the world.


The complete article: https://www.nature.com/articles/s41467-024-45812-z


This study explored harmonic relationships that are pleasant or unpleasant to our ears by having participants listen to “dyads” (two-note intervals) in which the sounds were manipulated in several ways.


First – by compressing or stretching the harmonic partials as shown below in order to learn how these manipulations affected the perception of pleasantness of the listeners:

Compressed and streched harmonic partial

Intuitively, this can be understood from the observation that interference is minimized when partials from different tones align neatly with each other (as in the harmonic sequence above). If we then stretch each tone’s spectrum, we must also stretch the intervals between the tones to maintain this alignment, meaning that the fundamental will stray from pure Pythagorean harmonics. Once the individual tones become inharmonic, the overall chord also becomes inharmonic, irrespective of the intervals between the tones.


The result therefore provides evidence that interference between partials is an important contributor to consonance perception.


The metallophones of Indonesian gamelans and the xylophone-like renats used in Thai classical music – each instrument has an idiosyncratic spectrum that reflects its particular physical construction, with potentially interesting implications for consonance perception. The study investigated an inharmonic tone inspired by one such instrument, the bonang, which uses the slendro scale.


The inharmonic slendro scale might be explained in terms of the consonance profile produced by combining a harmonic complex tone with a bonang tone.


The stretching/compressing manipulation is interesting from a modeling perspective, because it clearly dissociates the predictions of the interference and the harmonicity models (partials in defining pleasantness and unpleasantness is called “harmonicity”). It shows that only the former are compatible with the resultant scales. The latter manipulation is interesting from a cultural evolution perspective, because it supports the hypothesis that the slendro scale developed in part as a specific consequence of the acoustic properties of Javanese gamelan instruments.


The study found that manipulating the frequencies of the harmonics can induce inharmonic consonance profiles. If we stretch or compress this partial, we also have to stretch/compress the distance between the two tones in order to hear a pleasant harmony.


The second step is to enhance or cancel the harmonics in order to understand the role that these harmonics have in our judgment. First, the study considered how consonance profiles may be affected by changing the amplitudes of their tones’ harmonics. In particular, we focus on the so-called spectral roll-off parameter, which determines the rate at which harmonic amplitude rolls off (decreases) as harmonic numbers increase, by increasing the harmonic component:

The study determined no clear effect on pleasantness variability; the profiles remain highly differentiated for all roll-off levels.


Finally, they tested whether consonance profiles are affected by a more radical manipulation by completely deleting particular harmonics:

Deleted selective harmonics

Removing the harmonicity of the tones in fact reduces the straying away of the pitches from natural harmony.


In summary, the results point to an important contribution of harmonicity to consonance perception. It becomes clear that the upper harmonics of a tone has an important role in defining pleasantness in dyad intervals.


These results provide an empirical foundation for the idea that cultural variation in scale systems might in part be driven by the spectral properties of the musical instruments used by these different cultures. In Western culture, when the reference point is generally based on string instruments, the harmonic tone relationships are different than the ones from South East Asia. In Java, for example, tone relationships are based on Bonang – a collection of small gongs from the Gamelan ensemble, which have a very different series of harmonics or harmonicity, therefore ending up with very different scales used by both Western and South Asian cultures.


The Javanese slendro scale and the pelog scale, both of which are pentatonic, deviate considerably from the Western 12-tone scale.


On the other hand, it is interesting to know that this differentiation is not anthropomorphic: a Westerner listening to Bonang instruments would come to the same conclusion as a South East Asian listener regarding the pleasantness of an interval, and vice-versa. It is indeed the instrument and their specific harmonicity that defines the scale chosen.


So there you have it – the first study found universal relationships between song and spoken words; the second found a locality in the judging of pleasantness in harmonic relationships between tones, although this difference is environmental, not fundamental.


I hope that this will help us understand that in the end, we are the same and our similarities are more than our differences.

Who is ignorant of motion is ignorant of nature

Posted on by
Reply

The major contributions to science that Galileo brought to the world are well known. But putting these discoveries in the musical context could turn out to be more relevant that one would think.

The origin of Western science is linked to the study of harmony. As it was understood, Harmonia comes to be in all respect out of contraries; for Harmonia is the unity of multiplicity, and the agreement of things that disagree (the fitting together of extremes).

The Pythagorean school of philosophy sought to integrate scientific inquiry into the nature of Number and a mythical awareness of the musicality of universal law. In particular, the harmonic series consisted of whole numbers: 2/1, 3/2, 4/3, 5/4…and so on.

The instrument that was used to investigate numbers was the monochord (see my previous blog post on the subject), which is used to measure the relationship or ratios between harmonics of a root note (the fundamental).

In fact, some historians of science contend that the division of the monochord strings is possibly one of the earliest scientific-empirical experiments ever to be carried out with mathematical rigor.

Image of a monochord played by a monk

Throughout the whole of history, right up to the eighteenth century, the monochord was associated with cosmic concerns…the stretched string stood for the universe, with the various harmonics representing the planets in the solar system. Music, mathematics, and astronomy were inexorably linked in the monochord. The universe was thought to obey musical laws; therefore, the study of the monochord yielded information considered relevant to the other sciences, the humanities, and religion. Keeping with this harmonic-based cosmology, Kepler discovered a numerical relationship, his third law of planetary motion where the major semi-axis of the orbits of planets and their periods are proportionately related. He called it the “Harmonic Law”, and like all the philosophers of the time, he studied the ancient world of Pythagorus and Plato (Kepler also attempted to fit all the orbits of the 6 planets in nested Platonic solids).

Ancient cultures, before the invention of the printing press and the proliferation of books, were far more sonically oriented than visually focussed. That made them more receptive of the subtleties of the nature of pure tones.

Galileo was born into a musical family, and his father Vincenzio, beside being an excellent lutenist, was also a music theorist, and was investigating tuning. There was at the time a controversy about which form of tuning was best: on one side was the ‘natural’ tuning based on the harmonics of the monochord, and on the other side a more “tempered” tuning, which sounded more pleasing to the ears, in particular the major third- which sounded a bit harsh in the ’natural’ tuning. Also, the pure tuning limited the number of keys the instruments could play in. Galileo, who also played the lute, helped his father in his research. This research involved weighted strings which were set up similar to monochords.

There are several examples of how Galileo would have used music in his research:

In order to keep time while conducting his studies of the motion of bodies and their rate of fall, he used a ball rolling on an incline, by spacing frets at increasing distances from one another in order to hear a steady beat. If the frets were spaced evenly the ball would hit them at an increasing rate. At the time there was no clock precise enough to measure this. The obvious solution was music. Sing a song and the beat will be steady. This was first suggested in 1973 by Stillman Drake, a leading Galileo expert. 

After Galileo discovered the moons of Jupiter, he spent a long time figuring out their periods, in an unsuccessful attempt to use their orbits as a clock to help navigators establish their position at sea, since the first three moons- Io, Europa and Ganymede, were locked in a harmonic ratio of 4:2:1 at one octave from each other.

I think it makes sense to mention that during the experiment at the Tower of Pisa (if it ever happened), the sound of the two objects hitting the hard surface of the ground would have been much more accurately measured by the sound made than by looking at them. The rate at which our ears can distinguish singular events from one another is four times more precise as the one our eyes can.

So thinking about Galileo and the work he did assisting his father with tuning, I am sure his inquisitive mind must have stretched the boundaries of these investigations, and I dare to come up with the following insight:

Coming back to the experiment at the Tower of Pisa, I started to wonder if there was not some connection with the “weighted string experiment” which is how some monochords are set up: by hanging weights at the end of strings. And trying to understand what would be the common phenomena of the falling object and the production of the tones on the strings put into tension by the weights. It dawned on me that there could be a direct connection:

  • the weight (let us say they are stones), initially are at rest, and have potential energy, each linked to their mass
  • this energy is unlocked when put in motion, either when released from the top of the tower or from being hung from the strings they are attached to. None of the phenomenon in these configurations – the falling of the stones or the tones emitted by the strings in tension from the weights – are possible without gravity.
  • as the weight of the stones’ sizes differ, the tension on the string varies.
  • in order to reveal their tension, we have to pluck them, which gives them energy (the same goes for the stones- we have to nudge them over the tower’s edge to use gravity to put them in motion)
  • as it is apparent in the stones’ varying sizes, each string produces a tone that is proportional to the size (in that case inversely proportional, the smaller stone giving the lowest tone) of the stone
  • the energy given to the string manifested in its tension is equivalent to the energy produced by the gravity acting on the stone, both directly related to their potential.
  • you could assume that if you pluck two strings together, they should not reach our ears at the same time, as the lower frequency (being of a lower energy tied to the lighter stone) would take longer to travel in the air than the one with the higher frequency (tied to the heavier stone) as you would assume that the lighter weight would fall at a slower rate. But they don’t, they reach our ears at the exact same time (we never question this because it is so obvious). 
  • but both phenomena, the plucking and the falling, are merely a translation (or to use a musical term, a transposition) of the same initial fact: the size of the stones, and both are a form of motion. The only difference is that one (the sound waves) do not have friction (actually traveling through the medium of the air). So if we remove the friction on the stones, you should end up with the same result and they would hit the ground at the same time, as demonstrated by cosmonaut David Scott of Apollo XV on the Moon – as the different notes reach our ears at the same time.

So it could have been that this correlation was revealed to Galileo during the experimentations he performed with his father, and the root of these physics could very well be music. it seems to me that we have the same initial state give rise to a similar effect, demonstrated by two phenomena, connected through the bridge of the Monochord acting as a phase transition acting on the energy of the stone. 

The various stones fall at the same rate and the various sound waves travel at the same rate.

Of course these are conjectures; it might not be the way his train of thought worked out. But I think there is a chance, and it is an interesting proposition, and it shows that the Law of moving bodies can be deduced with this old instrument, the monochord.

To close, it is interesting to know that in the past ten years the relationship between science and music has been revived and has revealed to us elements in our data set that would not be so easy to discern if the information was offered to us visually only. There are many examples – from exoplanet systems, asteroseismology, gravity waves, and so on. (View my previous posts)

When you listen to the music of Galileo’s time, it is important to try to imagine what was the acoustic environment in which it was conceived and performed. It clearly illustrates the unique position he held in the history of human knowledge with one foot in the ancient world and the other in the modern world. He was, to use a trendy word, an inflection point not possible without the past but enabling the future.

Sounds from deep space

Posted on by
Reply

Since the detectors of the electromagnetic spectrum in which we bathe are receiving the full spectrum of its emissions, and since the visual part of this spectrum (the one we can see with our eyes) is only a small part of its range, we have to “transpose” its data so that we will be able to match our senses. This is usually understood as making it accessible to our eyes, as we are an intensely visual civilization. But the sound spectrum is increasingly being used, and there are several reasons for this development.

Originally the emphasis was to give access of the data to visually impaired by translating images into sounds. The basic principle is to render higher data entries into higher frequencies and the lower ones into lower frequencies, a result resembling sine wave (for example) will be translated in an undulating pitch recalling the sound of an ambulance siren (the European kind).

But in reality when you get a data feed from an observatory, the results are much more complex.

Most of the pretty pictures form space of nebulas and far-flung galaxies are in a good portion made by “transposition of data” that our eyes can’t see, and these can be sonified and the results can be as pleasing to the ears as the pretty picture you see in magazines or online.

But there are some data that is timed, meaning that they develop on a time scale. They are not still and instead of the picture, we need a video. For this kind of data, sound is as good or even better to understand with sonification, in particular to detect patterns. Here’s an example which represents Fast Radio Burst or FRBs for short, these are mysterious events from deep space, and I mean deep- billions of years in the past. They are massive explosions, most of the time one-offs, but some repeat. We have not yet understood what causes them; one of the explanations is that they could be from a rare type of star called a magnetar, which are collapsed stars with a very strong magnetic field. Here are two ways to represent them:

Video of the event

Sonification of the event:

You can judge as to which one conveys the jumps between high and low frequencies.

For another example: let’s look at data that is only usable using sonification:

One of the hardest things to find out about objects in the universe is to assess their distances. There are several methods that work for different distances: parallax, type A supernovas (also known as standard candles), redshifts, etc. I won’t go into details about these, but the farthest the objects are, the less accurate the distances are. Furthermore, it is important to be able to double check the results with at least two modes of investigation.

A new method to get information about these distances has been recently developed and it uses translating data into sounds. it is called asteroseismic parallaxes and it uses asteroseismology (the study of earthquakes in star or star quakes). These calculations were performed on over 12,000 oscillating red giant stars. 

The speed with which sound waves propagate across space depends on the temperature and density of the star’s interior. “By analyzing the frequency spectrum of stellar oscillations, we can estimate the size of a star, much like you can identify the size of a musical instrument by the kind of sound it makes – think of the difference in pitch between a violin and a cello,” says Andrea Miglio, a full professor at the University of Bologna’s Department of Physics and Astronomy who is one of the study’s author.

So by translating these frequencies into sound, we, now that we know their sizes, can deduct their luminosity. And by using their luminosity, it allows us to find out how far they are from us.

“In our study, we listened to the ‘music’ of a vast number of stars – some of them 15,000 light-years away!” says Saniya Khan, a scientist in Anderson’s research group and the lead author of a study published in Astronomy & Astrophysics.

you can read about it here:

https://actu.epfl.ch/news/scientists-measure-the-distance-to-stars-by-their-/

I’ll be interested in hearing this sonification. Once again, space is silent, but the symphony that all the electromagnetic spectrum sends to us in the form of photons, once transposed into the visual or auditive spectrum, carries a lot of valuable information. And it might even sound good.

Can we hear all sound waves?

Posted on by
Reply

The obvious answer is no, because some waves are at frequencies our ears cannot detect (about 30 Hz on the low end and 18 kHz on the high end, although most of us have a hard time hearing beyond 12 kHz). But this is only a very anthropocentric view. Many other species can hear way beyond the human range, the most well known being elephants on the low end and bats on the high end, and we don’t really know the full extent of the animal kingdom’s ability to hear the full range of sound frequencies.

But this blog is about the full range of sound waves we can detect, even the ones no living creature can hear. To achieve this, I need to make a very general and fundamental definition for this phenomena. Sound waves are, in their most basic definition, a form of energy transmission. There must be some kind of impulse before a sound wave is produced, as every musician knows – looking at your instrument will not produce a sound, no matter how much you concentrate on it. Strings need to be plucked, drums to be struck, and wind must be blown in your trumpet in order to produce a sound wave. In other words, energy has to be spent for the sound to be emitted and the wave to spread to your ears.

So- waves are energy in motion. But it is important to remember that there are two kinds of waves: sound waves and electromagnetic waves. The fundamental difference between the two is that the first needs a medium to travel in, and the second doesn’t. Both are waves, which makes them energy in motion. Electromagnetic waves create their own magnetic field, which allow them to travel through empty space. Sound waves have many mediums available for their transmission: air is the first that comes to mind. But let’s not forget that this applies to all of the gases, (interestingly, the latest NASA Mars rover “Perseverance” carries a couple of microphones and the recordings tell us a lot about the Mars atmosphere, its composition and pressure, and how the sound propagates), but solids also transmit sound at different rates depending on their density (the only way we know about the inside of the Earth is through sound waves). And not to forget the other medium of water, in which sound waves travel longer and faster than in the air.

Let’s not stop here! Stars have sound waves traveling through them; in fact, they ring like bells, and even minutes after the Big Bang, sound waves bounced around the plasma of particle soup that predates the formation of matter and may have been the kernels of density that allowed the stars and galaxies we see today across the universe to form.

Now we have reached the astronomy scale – the size in which the newest form of waves were first detected in 2016 (although these waves were predicted 100 years earlier, thanks to the theory of relativity). These are called Gravity Waves, and they are an interesting bunch, because the medium they travel in is literally the fabric of space-time, and there again are two kinds, the high frequency ones and the low frequency ones. Their range goes from the millisecond to years. They are created by the most energetic phenomenas in the universe: black holes and neutron stars. The shorter gravity waves come from the merger of these objects; and the longer waves by their orbits around each other.

We cannot “feel” them. These waves are extremely faint, but new instruments like LIGO in the United States, Virgo in Europe, and KAGRA in Japan are detecting them almost daily. There is an application that lets you know when one is detected. You do not feel them but the atoms in your body do, so you can shudder and be a bit thrilled to be a part of the universe in this way.

These gravitational waves are somewhat in between sound waves and electromagnetic waves, both traveling through empty space, but they tend to be closer to sound waves because they do need a medium to go through- although this one is the fabric of space, the same fabric that makes planets circle around stars.

To conclude, I would say that as I dig deeper in the wave phenomena, my title for this blog post has to be answered in the negative. In the process of answering the question, ‘can we hear all sound waves?’, I discovered that there are more sound waves than meet the ears. But we can transpose them and raise their amplitude, and partake in the symphony of the cosmos.

Here is the link to the gravitational-wave-events app:

https://apps.apple.com/us/app/gravitational-wave-events/id1441897107

More Megalithic Musing

Posted on by
Reply

My last post about the navigational Heiau called Ko’a Holomoana in Hawaii made me notice another megalith that could be described as “navigational”. Although the scale of the map it appears to refer to is not as wide as the Pacific Ocean, it nonetheless describes a large area.

In this post, I will be making a case for “Les Menhirs de Lutry” as a geographical alignment. This megalith is made up of large and not so large stones on the shore of Lake Geneva (or Lac Léman, which is how it is called in the area, a name that dates from the Romans – ‘Lacus Lemannus’ – from a couple of thousand years ago). As I understand, no one has ever published this interpretation, but it seems to be an oversight, and should at least be contemplated as an explanation of its unique layout.

Megaliths come in many shapes and forms, and their interpretations are a part of guesswork and careful investigation of their geographic situations. There are two main categories that often overlap: they can be ceremonial, such as for a burial or place of ritual; and/or cosmological in their intent, meaning they are astronomical alignments which are in use as a calendar where the heliacal rising and setting of stars is marked, and allows for the study of the motion of planets, stars, the Sun and our Moon.

The finding of the navigational Heiau in Hawaii, and now the possible representation of this alignment of stones in the town of Lutry might elude to a third category, which could be named “geographical” or geodetic. 

Full disclaimer: obviously, I am not trained as an archeologist. I am just curious about astronomical alignments that megaliths often demonstrate. This kind of cosmological stone construction is most often found in two typical layouts: rings or circles (like Stonehenge in England), or straight lines which are often parallel (like Karnak in Normandy). The stones in Lutry are loosely aligned with the summer and winter solstice, but their alignment falls in between the two typical layouts – the Lutry megalith stones are placed in a row; but at some point they bend to the south, as you can see in the image below:

Layout of the stones at the “Menhir de Lutry”

Secondly, there is a vertical progression, as the eastern part is composed of larger and taller stones that progressively get smaller as it moves to the west and starts bending to the south, as shown in the next image:

The alignment is on the shore of Lac Léman, and across this body of water, a large massif of Prealps mountains dominate the horizon. Unfortunately, due to the fact that the monument sits in the middle of a small town, this imposing view is obscured by houses and therefore separates the geographical features that these stones are representing. In order to recreate the original setting, I scanned the alignment and placed it in plain view of the landscape as it would have been originally. I removed the houses and placed the monument as it would have looked when it was built:

“Menhir of Lutry” with Building removed

Each stone matches a large mountain block, and as the mountains recede, the stones get smaller. There are two stones that must have been lost through time. When we take a different view from above, there is more that matches the geography. As we see in the plan above, the stones bend to the south as they get smaller. This replicates quite accurately the natural bend along the south shore of the lake as it it moves to the west. To highlight this, I have highly magnified the stones to show how accurately they match the curve of the lake.

Les Menhirs de Lutry” from above (the south shore of the lake is on the top of the image)

Here is another view from the south

“Les Menhirs de Lutry” view from the south and at an angle  (the north shore of the lake is on the top of the image)h

These two montages highlight the close match between the alignment of the stones with the shoreline of the lake. The combination of the silhouette view of the mountains as shown in the first montage with the stones matching the curvature of the shoreline shown from above in the second and third, reinforces the theory of intentional map making.

The question then arises: why would the builders of this megalith need to build such a representation of the mountains and lake shore on their side of the lake? Obviously, we don’t know; so I ask myself, why do we use maps at all? Especially such a large map that obviously we cannot fold and transport in our backpack? These kinds of maps are used in situations (i.e. situation room) where we need to plan some kind of collective action: hunt, prepare for war, celebrations, exploration – where you want to coordinate and plan the movement of a number of people.

It could also be that these mountains and this lake have mythical meaning to the megalith builders, and to recreate it in a more manageable scale, it allows them to have some control over the elements. The alignment seems to not have any particular astronomical alignment – it does not face east or west, where most celestial movements occur and are more obvious.  

So, is geographical mapping a category for these megalithic structures? I first experienced one, as I mentioned above, when visiting the navigational Heiau on the Island of Hawaii, a megalith that maps the major islands of the Pacific Ocean. It seems to me that Les Menhirs de Lutry appear to follow that pattern. If this theory holds, it shows that the builders of these ‘geographical megaliths’ had some impressive geodetic knowledge and abilities.

A Cosmic Misunderstanding

Posted on by
Reply
Navigational Heiau called Koʻa Holomoana

During my second trip on the Big Island of Hawai’i, a trip that turned out to be as spectacular as the first one, was made quite unique by the fact that the Mauna Loa volcano started erupting the day we arrived. This made me quite happy, especially since the weather predictions were not looking too good for the week. If I was not able to see and photograph the fire in the sky (i.e. stars), I would get to see it coming out of the ground. But this post will not be about this event, but about the ongoing controversy regarding Mauna Loa’s neighbor volcano Mauna Kea and the telescopes sitting atop it decoding the universe.

Mauna Kea with the observatories at the top

At the time of our first trip we got to visit two of these “big eyes” (the Keck and the Infrared telescope). We were made aware of the tension that had arisen between the astronomy community and the native Hawaiian community around the building of a new large instrument Named the TMT (Thirty Meter Telescope) that would be added to the top of the mountain. In an act of protest, a group of native Hawaiians blocked the access road as the first construction trucks attempted to reach the summit.

The Thirty Meter Telescope (TMT)

The source of the dispute has many layers, but the underlying reason comes from the fact that Hawaiian natives have been dealt a most unfair deal by the United States. First, as in many other instances, by taking over the Islands and secondly, by forcibly making Hawai’i a part of the United States without asking the opinion of its future citizens. These actions had the consequence of diluting and marginalizing the original Hawaiian culture. So when the planning of the TMT (as well as for the current collection of observatories) was put in motion, no effort was made to include the local population in the discussion and planning. This ignited a longtime resentment and a feeling of cultural subservience to the “Western World” embodied by the invasion of the summit, which they consider sacred.

Mauna Kea with the glow of the Mauna Loa eruption

In recent years, the astronomical community has realized that there would be no possible agreements on the matter until an effort of outreach was made, and has begun to remedy the problem with educational efforts and acknowledging Hawaiian culture by naming objects discovered by observatories on the mountain in the native language (‘Oumuamua, our recent outer-solar visitor being the most famous). But a vocal minority has not yet accepted the construction. They view the collection of observatories as desecrating their holy mountain for an application that does not concern them. The top of the volcano represents their connection with their gods, and the connection of two worlds: Earth and the Heavens.

But Is there no possibility that the native Hawaiians can find a path to accept the observatories in a way that coincides with their tradition and cosmology?

I think there is, and I propose that by looking at the past history of the islands, and by a study of the lost Hawaiian knowledge of the stars and geodesics, it can be demonstrated that these two cultures both have the same goal in mind and that their achievements are not so far apart.

On the west coast of the Big Island sits a unique monument, a navigational Heiau called Koʻa Heiau Holomoana. A Heiau is a temple or place of worship where native Hawaiians held ceremonies. Several Heiaus were destroyed at the official end of Hawaiian religion (Kapu system) after the Battle of Kuamo’o in 1819 and the long shadow of influence by Christian missionaries. There are many Heiaus on all the islands, but, as far as I know, none that resembles this unique one.

This picture shows clearly the curve of the hill at the Navigational Heiau

The monument consists of a series of upright stones, not unlike megaliths found around the world. Each stone serves as a unique marker that points to the direction of an island in the Pacific Ocean. Early Polynesians were guided by an intricate navigational system using the constellations, and it is how the first inhabitants of the Hawaiian Islands (about 1500 years ago) sailed to them. This knowledge has been lost to modern day Hawaiians, although it is enjoying renewed interest in recent times.

Navigational Heiau from the road

Unfortunately there are no studies that I could find about this Heiau. The only information I found comes from a great guide book about the island by Andrew Doughty, who investigated the monument and connected the stone markers with specific islands in the Pacific, using GPS data and aerial photography to reveal the alignments (in the app accompanying the book he tells a pretty interesting story about his investigation).

I visited the Heiau last month, and it was a bit difficult to find as there are no markers indicating the path to it, but you can see it from the highway – so on the second try we found it. The Heiau sits on a round hill overlooking the ocean, an unlikely spot for a Heiau, as all the ones I am aware of seem to sit on a flat surface. As I was looking at it trying to imagine how it could have been used by the ancient navigators, I realized while looking at it from the back of the monument facing the ocean that I could not see all the markers, as some were hidden by the curvature of the hill. It took me a while, but back in New York while working on the photos I took that day, it hit me: what the curvature of the hill recreated was the curvature of the Earth! So it is a 3D representation of the Pacific Ocean.

A 3D scan of the Navigational Heiau

Well, these are conjectures on my part, but it makes it pretty clear to me that the ancient Hawaiians must have been aware that the Earth was round. As it was already known, they were aware of the motion of the stars in the heavens, but in this instance it seems that they were able to make a model of it. This knowledge is evidence of very careful observations made over many centuries traveling throughout the Pacific Ocean. In this there is a direct connection between the observatories atop Mauna Kea. In fact, knowing about the curvature of the planet is a prerequisite in order to understand our place in the cosmos and to be able to map it. 

As I mentioned earlier, most of that navigational knowledge has been lost. To rediscover it and promote it would go a long way in harmonizing traditional and western cultures using a community of goals with a variety of means.

Link to the Mahukona Navigation & Ecological Complex site

Department of Land and Natural Resources of Hawai’i
Office of Conservation and Coastal Lands

About the Thirty Meter Telescope

The Monochord

Posted on by
Reply

The Monochord.

Fotothek_df_tg_0006260_Musik_^_Harmonik_^_Monochord_^_Einsaiter

Until recently, I had some difficulty explaining the origin of the link between music and science. Of course, I understood this deep connection, that frequencies are ultimately numbers, and they relate to each other in rational intervals. This understanding is due to the fascinating fact that the ear has both qualitative and quantitative abilities: it has the ability to understand the moods/colors and the ratios of sounds. This ability makes it a pretty unique sense; in fact, it is the only sense that can accurately measure and “feel” at the same time.

But this did not explain that since antiquity, music was made an equal to geometry, mathematics and astronomy (The Quadrivium); it is only recently in the modern era that we are able to understand frequencies and compute them, and this is only made possible by the use of scientific instruments. Although ratios between the partials were understood to be rational in their fundamental nature: 1:2, 2:3 and 3:4 for the octave, 5th, 4th, and so on, that knowledge dates from antiquity. But how did this realization come about? I was aware of the monochord but I took it as a demonstration tool, illustrating the phenomena of musical ratios. I had it wrong: the monochord is not the message, it is the medium. It is the “instrument” that led to this discovery, and in fact, the monochord is the first scientific instrument which allowed accurate measuring of a physical phenomena, to display geometrically these acoustic relationships and to translate them mathematically. The origin of the monochord is unknown: “the Greeks attributed its invention to Pythagorus; however, like most musical technologies it was probably imported from Babylonia or Egypt…No more accurate tool for investigating musical tuning was invented after the research of Helmholtz in the later half of the nineteenth century.” [An Introduction to the Monochord, Seimen Terpstra]

Modern monochord with four strings

Modern monochord with four strings

Initially what the monochord was able to investigate is the rational division of the whole. This term is taken as “wholly” a quasi-“god”- like concept, in a cosmological sense. In other words, the rational division visually demonstrated by the placement of the “bridges” dividing the strings at various divisions of the “whole”, illustrated the inner working of the cosmos, revealing the inner harmonies of the world that were at the core of philosophical inquiry up to the nineteenth century.

Back in antiquity, truth for the Pythagoreans manifests itself through the world of physical phenomena. (Fideler in Guthrie, 1987) “The Number was the essence of a sacred order, and nowhere was this better expressed for the Pythagoreans than in cosmic music, paradoxically unperceivable because [it was] permanent.” (“Star Music”, Eduard C. Heyning, 2017)

“As the eyes are designed to look up at the stars, so are the ears to hear harmonious motions; and these are sister sciences – as the Pythagoreans say.” (Plato Republic VII 530d; 1937, I. 790)

Boethius

Boethius

“The ears of mortals are filled with this sound, but they are unable to hear it….The sound coming from the heavenly spheres revolving at very swift speeds is of course so great that human ears cannot catch it; you might as well try to stare directly at the sun, whose rays are much too strong for your eyes.” (Cicero, The Dream of Scipio),

So this music of the spheres is music that we cannot hear because we’ve been hearing it since birth. Only the semi-divine Pythagorus could, and he was able to make us hear and see on a string, this music to which the planets of the solar system who can be made to intone a dominant chord, (see “Waves Passing in the Night”, Walter Murch). What can it reveal to us?

Kepler 3rd (Harmonic) law

Kepler 3rd (Harmonic) law

Closer to us in history, Johannes Kepler is the one who began to bridge the two world views of wholistic antiquity and the birth of modern science. Kepler is a “rational mystic”: in one way looking back over the centuries to the platonic theories, and in the other, laying down the laws of planetary motion which generated the foundation for the future work of Newton on the laws of gravity. This is culminated in Kepler’s third law, which rules that the ratios between the semi-axis (half the diameter) of the orbit of a planet and the period (a planet’s path around the Sun in a year) is harmonically related (r3= P2). This third law of Kepler’s is called “the harmonic law”, which has one foot in antiquity and the other in the modern world. 

As it turns out, many examples of harmonic relationships exist in astronomy. The most evident example that illustrates this relation and that we can all witness in the sky, is the 1:1 relationship locking the Moon to the Earth (one revolution = one rotation) so that we can only see one face of our satellite (incidentally, many exoplanets are gravitationally locked to their stars); another more distant example are the three inner moons of Jupiter which are in a 1:1, 2:1 and 4:1 harmonic lock, with their rotation also, like our Moon, on a 1:1 relationship with their revolution around Jupiter.“Jupiterians” would see only one side of each of these moons.

These relationships arise from the reciprocal gravitational influences of these celestial bodies; although they are harmonic in essence, they arise from different processes than musical harmonics. On the other hand, both share a surprising consistency with whole numbers.

Pythagorus

Pythagorus

Further numerical musings about whole numbers and speculations have been made, and are probably the root of numerology. Pythagorus was obsessed with whole numbers; he realized that the sum of 1, 2, 3 and 4 make 10 and went on from there to many speculations about the number ten. Of course there is the theorem that bears his name: 3² + 4² = 5² which probably set the standard for “beauty” in mathematical formulas. Going back to the monochord, my point is that simple rational relationships of integers are at the base of both music and science – astronomy in this case, and that, interestingly enough, in the process of codification of these disciplines, music did precede or at least showed the way.

These whole numbers are in use in the ratios visually displayed on the monochord from the root, fifth, fourth, third and so on to build scales…as 1, 2, 3, 4… although to say the astronomical and musical harmonics are one and the same seems enticing, until we understand more about both phenomenas, the jury is still out. Also, it is important to note that there are many incommensurablities. The “pythagorus comma” is a good example (the sum of twelve fifths = B#; this does not add up to the sum of 7 octaves = C8).

To summarize, these “explorations” were initiated with this perfect hybrid: the monochord, which is an “instrument,” a word used both to describe the tools to conduct science and music, and are etymologically linked for a good reason.

A world where sound is a mystery

Posted on by
Reply

I came across a powerful analogy, I was listening to a discussion a series of talk called “Conversation on the Nature of Reality” from the New York Academy of Sciences. The whole point of this talk is understanding the meaning of mathematics in society, is mathematic constructed or is it discovered. This is an age old puzzle, where do insight in the nature of things come from explained by the workings of mathematic coming from intuition, visualization in the mind the mathematician, and then laid out in formulas, which make sense to only a few.

We are blind to these insight, it is we cannot see them. We go through the world with the perceptions that we need to go on our daily musings, sure our life has been improved by our deepening understanding of the mysteries of nature. But how to understand this process, how make us un-initiated imagine what is going on.

An attempt at an explanation was proposed by theoretical physicist S. James Gates Jr. during that aforementioned discussion, and it is one that us musicians can have a particular advantage in understanding. Imagine a world without sound, not that it cannot exist, but that it has not been experienced yet. Some of the inhabitants of this far away world, who are like us thinking beings who share our ability to imagine, start to hear in their minds ear sound, not unlike when composing music earthlings hear it first in their mind before putting it down to paper, and by reflecting on their insight find a way to write musical scores to describe what their intuition has lead them to discover. To anyone else these “scores” mean nothing, they question the “musicians” what do they mean, and how did they came up with these notions, they ask does music exists as a separate physical fact and they are discovering it, or do the musicians are constructing it?

These same questions arise when we think about mathematics: is it there to be discovered or is it a construct of the rational mind as an attempt at understanding the physical world? Has music always been there and we are just discovering it, or are we creating it. The link between music and physics started when Pythagoreas  to his own amazement, discovered that the ratios of partials of a tone are whole numbers; 1,2,3,4,5,… In a linear progression.

I find this particular story to be a particularly interesting parallel; the formulas of mathematics are the scores of that mind insight, they are symbolic representation system that describe what we cannot see, hear or touch: mathematics. The same thing applies to music: we could not see, hear or touch music in a world without sound.

This also leads us to a fascinating conclusion as the other participant in the discussion science writer Margaret Wertheim, pointed out: by inverting the argument we can say: scoring music is only one way we can learn and appreciate music, there are countless musicians throughout history that do not read music, so if the parallel holds between mathematic and music understanding the equations should not be a prerequisite to understanding mathematics, and that brings us to the conclusion that as music mathematics can be understood intuitively.

Of course this is a “thought experiment”, it would be hard to find a world without this very important physical element. But it might be that this world is just space, like the one that separates us with the rest of the universe, and in interstellar space there is no medium, so no sound.

Here is a YouTube link to: The Mystery of Our Mathematical Universe

Moon in the News

Posted on by
Reply

Thanks to the Chinese, the Moon is back in the forefront of the collective mind. Of course every news show is reporting it, and the usual headline is:

Chinese land a probe on the Dark side of the Moon.

Only one problem with that statement: there is no such a thing as the “Dark” side of our beloved satellite. Like the Earth, the Moon has days and nights, and no side is privy to one or the other.

The Moon does rotate once a lunar month (from full to new Moon) about 28 days so only about half of that time is the “Far” side in the dark, same for the “Near” side. That is why we cannot see it when the “Near” side is at night time.

I guess Pink Floyd is probably to blame for a good part of the confusion but it’s not a reason (even if you are a die hard fan) to perpetuate such an inaccurate notion. And now that the Moon is back in the news, and appropriately, the Chinese rover is on the erroneously named Far Side.

By the way just look at the pictures it sent back- it looks pretty, should I say, sunny…

I rest my case.

Moon Phases

Moon Phases (click the image for a in deft explanation of the Moon phases)